That puzzling double-slit diffraction experiment
The Story
Many years ago, a series of double-slit diffraction experiments claimed to show that focused human attention could influence the interference pattern of photons in a laser beam. The researchers later reported confirmatory results using the same experimental setup.
Upon reviewing their first publication, I identified that their reported experimental parameters and graphical data conflicted with fundamental predictions of double-slit diffraction. The described setup appeared physically implausible and scientifically inadequate. I published an initial review documenting these issues.
One of the co-authors later in 2012 acknowledged—privately—that my correction to one of their key parameters (the distance D, as shown schematically in Figure 1) was accurate. Approximately a year later, the team, in a new configuration, published a follow-up series of experiments using the same setup. In that publication, they issued a correction to the value of D.
However, their published "correction" did not match the previously acknowledged correct value. Instead, it introduced a new, equally incorrect value—curiously, an anagram of the original erroneous D. This raised concerns that the original error had been strategically retained under the guise of correction, framed as a typographical oversight.
Despite this second adjustment, the new value for D remained inconsistent with the reported data, figures, and the underlying physics of double-slit interference. Regardless of the revisions, the reported parameters remained incompatible with the diffraction theory they invoked to support their hypothesis.
The Revealing Evidence
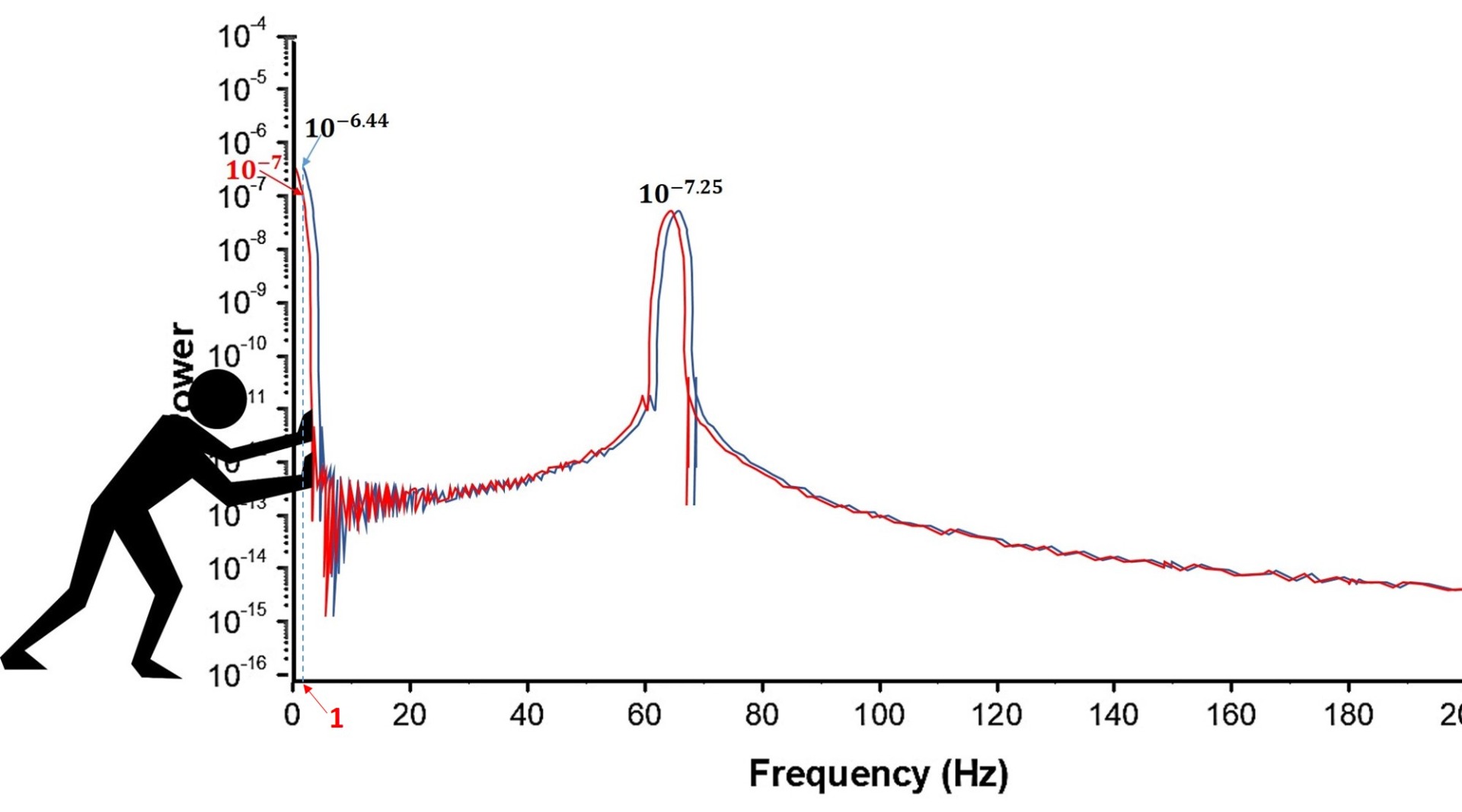
Extending my investigation, I presented further discrepancies in the published data and graphs through a series of videos. These illustrate how a deliberate shift in the Fast Fourier Transform (FFT) spectrum—central to the analysis of the double-slit diffraction pattern—can create misleading evidence in support of the tested hypothesis (see Fig. 6). In the published FFT graph, the entire spectrum is visibly shifted, producing a one-unit frequency gap at the origin of the frequency axis. This gap cannot be accounted for by the physical principles of diffraction or by the stated experimental parameters. However, it is consistent with an artefact introduced through computer programming.
A simple command embedded in the software performing the FFT analysis could artificially shift the spectrum during selected sessions—namely, those testing the Mind-Matter Interaction hypothesis. This shift alters the spectral power at a chosen frequency (e.g. one unit), thereby modifying the key measure (R) in favor of the hypothesis (see Fig. 6).
In Detail
The key measure R is defined as the ratio of two spectral powers (see Figs. 4 and 5). The denominator, P(1), represents the spectral power at a frequency of one unit and remains constant throughout the experiment, reflecting the steady laser intensity through the two slits. The numerator, by contrast, represents the spectral peak and should vary only if the interference pattern is altered.
In theory, a genuine decrease in R would require a reduction in the spectral peak power. However, R can also be artificially lowered by shifting the FFT spectrum: this causes the otherwise fixed denominator P(1) to increase (owing to the spectrum's shape), while the numerator remains unchanged (see Fig. 6). This deliberate spectral shift mimics the signature that proponents associate with a hypothetical mind–matter interaction—often framed in the jargon of consciousness-driven wavefunction collapse.
The program could introduce a randomized spectral shift between 0 and 1 frequency unit at the onset of each "mental effort" session, The altered spectrum would then produce a new, inflated value of P(1), lowering the value of R in a way that falsely supports the hypothesis.
The extent of the spectral shift—controllable by software—directly determines the strength of the apparent effect. For a full one-unit shift, as shown in Fig. 6, the resulting reduction in R reaches 71%.


I also explained how the false data they reported could arise from careless and poorly controlled experimental protocols—conditions unsuitable for sensitive laser-based measurements or any rigorous scientific investigation. The absence of strict procedural standards, combined with susceptibility to human bias, is a well-known source of unintentional error in experimental research. However, certain anomalies—such as the consistent spectral shift and the misuse of reported parameters—cannot be explained by carelessness alone.
How the Experiment Should be Prepared and Performed
Before the experiment-Checklist for Reliable Double-Slit Diffraction Measurements
A. Ensure the camera sensor window is clean so that all pixels — including those near the edges — respond uniformly to incident light and convert it accurately into an electrical signal.
B. Confirm each experimental parameter (wavelength, slit separation, slit width, pixel size, and slit–camera distance) by direct measurement or reliable documentation before reporting them. Using unverified or incorrect specifications undermines scientific credibility.
C. Adjust the slit–camera distance so that the central diffraction band spans the full sensor width. If the slits are too close, the band is narrower than the sensor, the fringes are compressed, and FFT analysis becomes unreliable. If too far, the band is wider than the sensor and some fringes are lost. For the parameters used here, the ideal distance is about D=16.6 cm (contrast this with the reported 10.4 cm, 14.0 cm, and the actual 15 cm). This produces a well-matched projection and ensures reliable fringe spacing and frequency estimation.
D. Orient the double-slit precisely perpendicular to the laser beam and center the diffraction pattern on the sensor. Proper alignment yields a symmetric interference pattern with the central maximum located at the middle of the sensor.
E. Confirm the pixel dimensions of the camera directly from the manufacturer's specifications before publication. Reporting an unrealistic pixel size undermines the credibility of the entire experimental report.
Reporting incorrect experimental results
A. The reported FFT spectrum exhibits an artificial one-unit frequency shift that cannot be explained by the physical properties of the optical setup. This spectral adjustment creates the false appearance of support for the hypothesis that human consciousness influences photon behavior.
B. The double-slit diffraction configuration was reported with inaccurate experimental parameters and demonstrated poor alignment and adjustment, undermining the validity of the results.
C. Given the inconsistencies in both methodology and data, the researchers—recognizing that their results did not support the hypothesis—should have acknowledged this clearly in their original publication, in their subsequent confirmatory reports, and in their responses to statistical critiques. A delayed admission of the lack of evidence—appearing only after public exposure through accessible narrative analysis aimed at a broader audience—remains scientifically and ethically questionable.
As Richard Feynman* famously stated:

This principle represents a fundamental standard of scientific practice—especially when claims challenge established physical theory.
*Richard P. Feynman. The Character of Physical Law (Penguin Books Ltd, Middlesex, England, 1992, p. 148).
The Double-Slit Diffraction Experiment in Six(+) Graphs
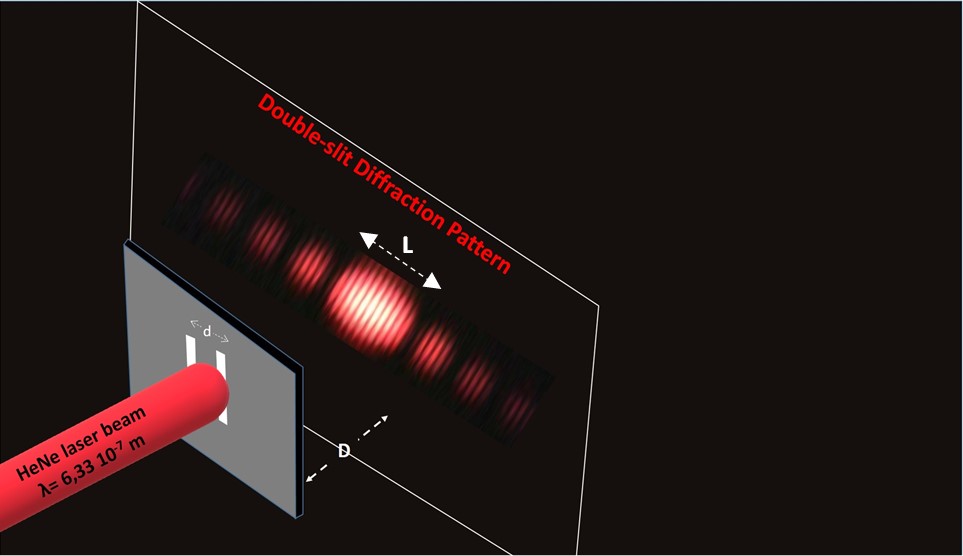
Figure 1. A schematic representation of the double-slit diffraction experiment. The double slit diffracts the HeNe laser beam of wavelength λ=632.8 nm passing through it. Each slit has width (a). The separation of the two slits is (d). The diffracted light pattern, an array of dark and bright regions with fringes within the latter, is projected on a screen (or a camera window) at a distance (D) from the double-slit.
The brighter central area with fringes is the central diffraction band of width (L). The number of fringes N in the central diffraction band depends on the ratio d/a. If d/a = 20 then N = 39:
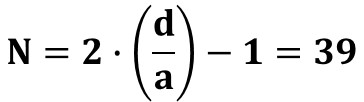
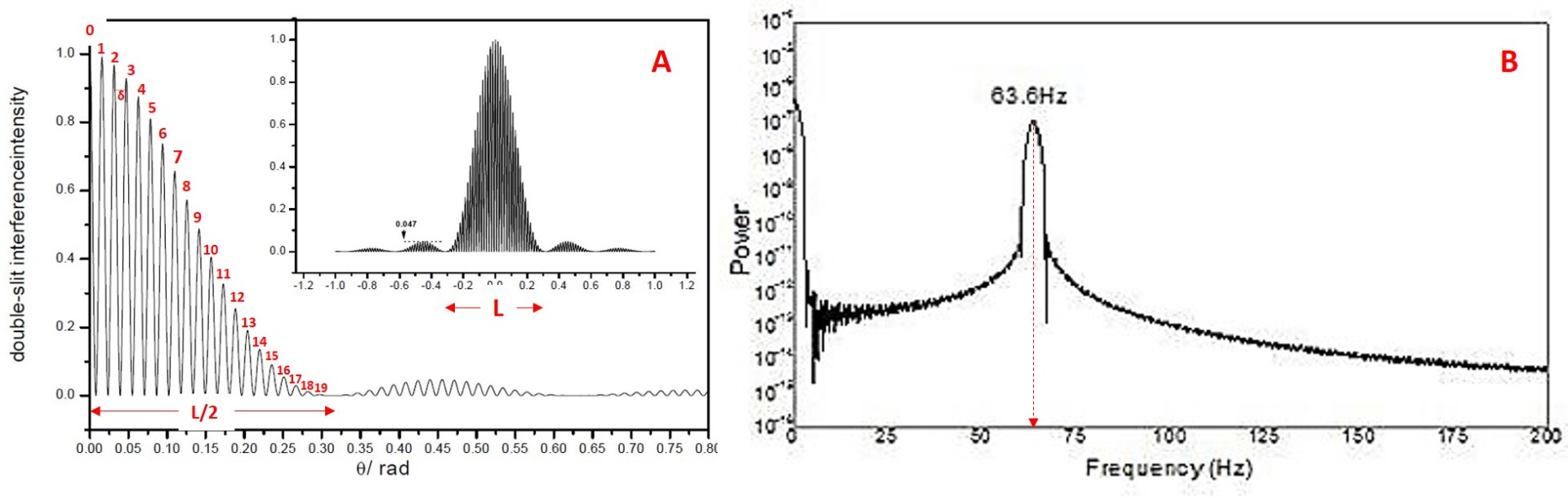
Figure 2. (A). Example of a computer-simulated double-slit diffraction pattern with a characteristic ratio of d/a=20, as explained in Fig. 1. It displays the light intensity variation across the pattern. The magnified half of the central diffraction band is on the left. The inset shows the full double-slit diffraction pattern.
Science-assisted 'clairvoyance'—"Viewing" the setup parameters from a long distance.
A double-slit experiment that produces a central diffraction band allows for a sufficiently accurate estimation of the fringe spacing, δ (see Fig. 2A). Even without direct access to the experimental setup, a scholar can determine the distance D between the slits and the screen (or camera) by substituting the estimated δ—along with its uncertainty—and the known experimental parameters λ (wavelength) and d (slit separation) into the standard diffraction relation:
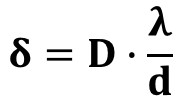
In the current example, which is a computer simulation, the spacing between fringes is approximately 0.0157 radians (in angular units).
(B) The Fast Fourier Transform (FFT) spectrum of the simulated double-slit diffraction pattern. The Y-axis of the spectrum represents the power associated with periodic components in the diffracted light. The X-axis corresponds to their spatial frequencies.
The prominent spectral peak at 63.6 Hz arises from the periodic structure of the interference pattern, determined by the fringe spacing δ produced by diffraction and interference through the two slits.
The frequency, F(K), of the dominant spectral peak is the inverse of the fringe spacing
δ:
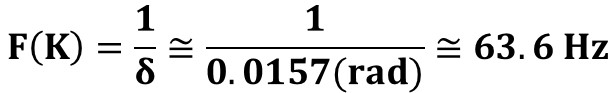

Figure 3. Table of the Fast Fourier Transform (FFT) frequencies and their corresponding powers. (Pallikari, 2012*). The Fast Fourier Transform (FFT) applied to the diffraction pattern from a double-slit experiment yields distinct spectral components. Each frequency corresponds to a physical feature of the diffraction and interference pattern captured by the camera. The key frequency components are interpreted as follows
P(0). The spectral power at zero frequency, P(0), represents the total light intensity recorded by the camera. It corresponds to the DC component of the FFT and reflects the overall brightness of the diffraction pattern.
P(1). The
spectral power at one frequency unit, P(1), corresponds to the light intensity
I(0) passing through the two slits, where I(0) = I₁ + I₂. It relates to the
broad modulation envelope of period L across the central diffraction band,
produced by single-slit diffraction. Since the optical setup remains fixed,
P(1) remains constant during the experiment:
P(1) = constant.
P(K). The prominent peak power P(K), at frequency F(K), arises from the periodic fringe structure of spacing δ within the central diffraction band. It reflects the fringe visibility (V)—the contrast between bright and dark interference fringes due to two-slit interference
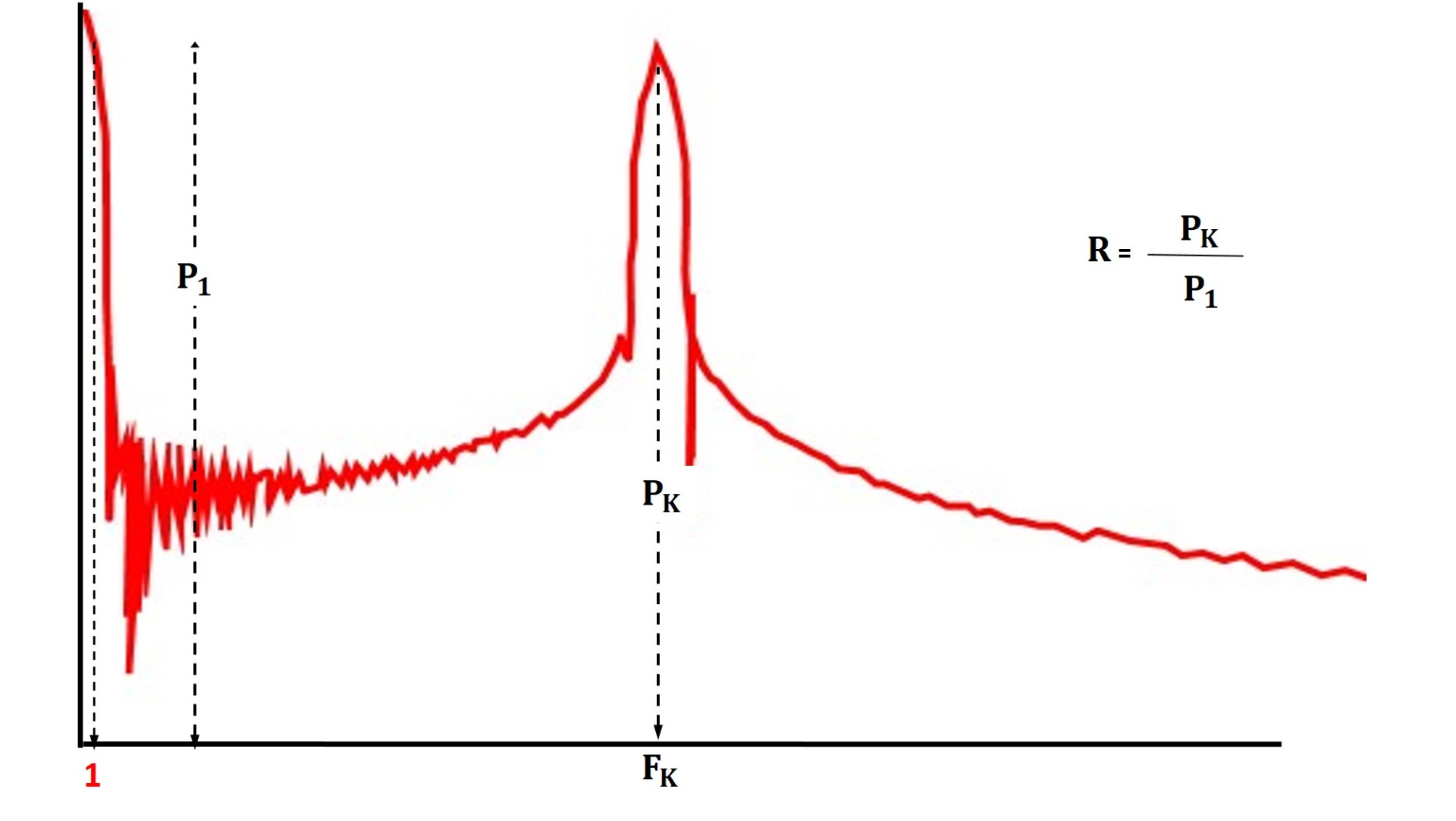
The ratio of spectral powers P(K) to P(1), referred to as the measure (R) (see Figure 4), equals the square of the fringe visibility: R = V²
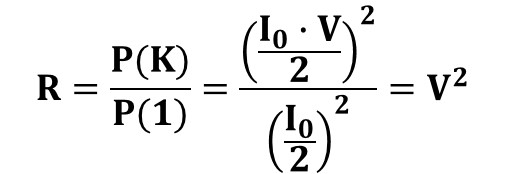
Objective of the Experiment
The double-slit experiment investigates whether human intention can reduce the spatial coherence of light, as indicated by a decrease in the spectral ratio R = P(K)/P(1). In parapsychological terms, it tests the so-called "Mind–Matter Interaction hypothesis."
The Reasoning
If the mind interacts with matter—specifically by disrupting the spatial coherence of diffracted light—then the fringe contrast (V) should decrease. This reduction in the fringe contrast leads to a corresponding decrease in the spectral peak power, P(K). Since the reference value P(1) remains constant*, the spectral measure R = P(K)/P(1) will likewise decrease.
Accordingly, to test for a Mind–Matter Interaction, the experiment seeks a systematic reduction in R during intervals of focused mental attention.
(*) On the question of wavefunction collapse in a double-slit diffraction experiment, Fotini Pallikari. (2012). arXiv:1210.0432 [quant-ph], https://arxiv.org/ftp/arxiv/papers/1210/1210.0432.pdf).
FIGURE 4. The Fast Fourier Transform (FFT) spectrum of the double-slit Diffraction Pattern showing the spectral powers P(1) and P(K).
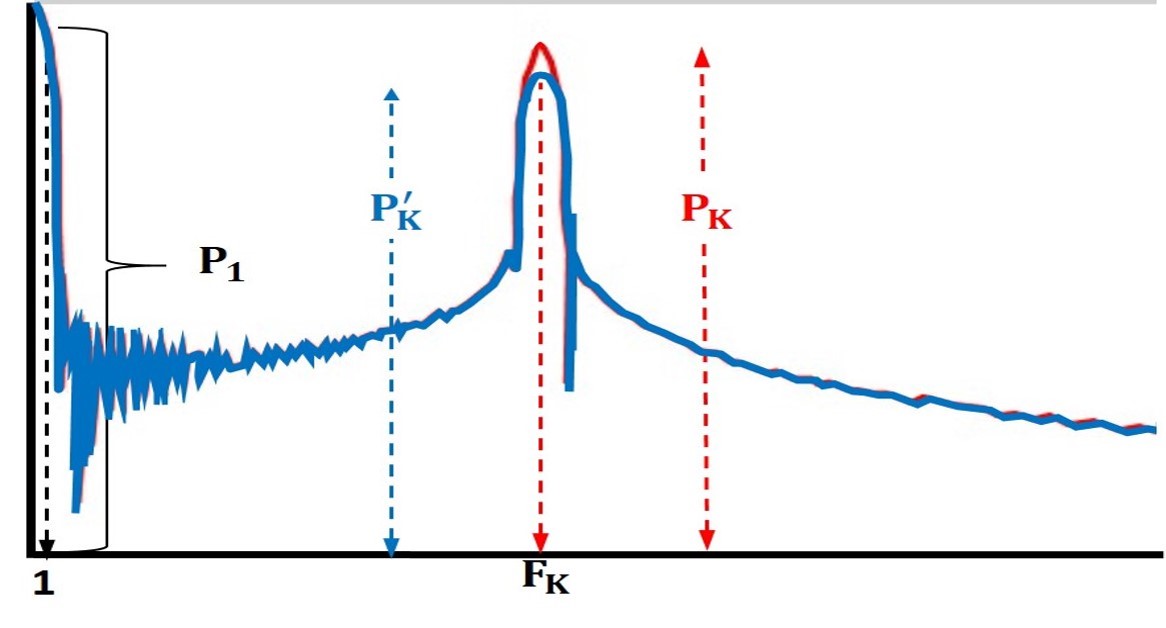
FIGURE 5. Observing evidence for Mind-Matter Interaction on the FFT spectrum.
If the mind interferes with the (spatial) coherence of diffracted laser light, the peak power decreases from P(K) (red curve) to P'(K) (blue curve).
As P(1) in the denominator of (R) does not change, a possible mental interference will cause the key measure (R) to decrease, a situation often termed, somewhat inaccurately, as 'collapse of photon wavefunction'.
FIGURE 6. An example of generating evidence for Mind-Matter Interaction in the double-slit diffraction experiment through experimental misconduct.
Suppose the power at the peak P(K) does not decrease during sessions when participants mentally attempt to interfere with the diffracted light. The key measure (R), as the ratio of two powers, P(K)/P(1), offers an alternative for inducing its decrease by increasing the power at one unit of frequency P(1). The technique is outlined in Fig. 6.
In the current example, the spectral peak at its proper position (red curve) is at a frequency F(K) = 63.6 Hz. Its spectral power, P(K), is ten to the power of -7.25. The power at one unit of frequency P(1) is ten to the power of -7. The key measure (R) is then 0.56, as the ratio of the two powers P(K) and P(1):
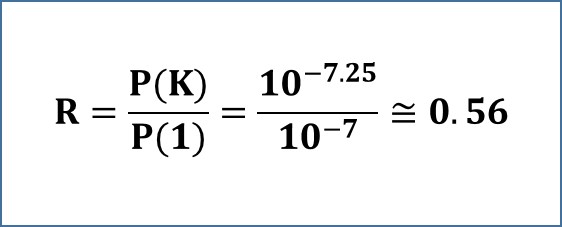
Let us shift this FFT spectrum to the right by a tiny amount of one unit of frequency. The peak at its new position has frequency (K') increased by one unit, becoming 64.6 Hz (blue curve). The peak power, P(K'), will be the same as before the shift, ten to the power of -7.25.
Due to the steepness of the spectrum at low frequencies, the spectral shift will force the power at one unit of frequency to increase. It is now ten to the power of -6.44. The shift will affect the key measure, which becomes (R') = 0.16.
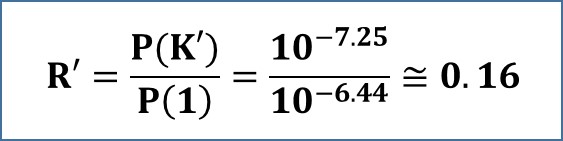
The tiny spectral shift forced the key measure (R) to decrease from 0.56 to 0.16, causing it to drop by 71%.
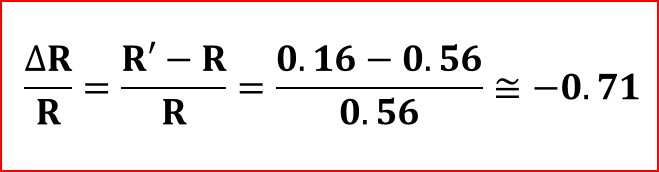
A one-unit spectral shift introduces the maximum possible artificial reduction in the key measure R—in this example, a 71% decrease, determined by the specific shape of the FFT spectrum.
Any smaller shift between 0 and 1 frequency units will produce a smaller reduction in R.
Most importantly:
Even a partial spectral shift—easily implemented programmatically—can significantly reduce R and thereby produce deceptive evidence in support of a mind–matter interaction or, in the language of quantum interpretation often invoked, a consciousness-induced wavefunction collapse.
Spectral Measures Can Be Artificially Altered by Minimal Shifts
Graph (A). Logarithmic Increase in P₁ with Frequency Shift:
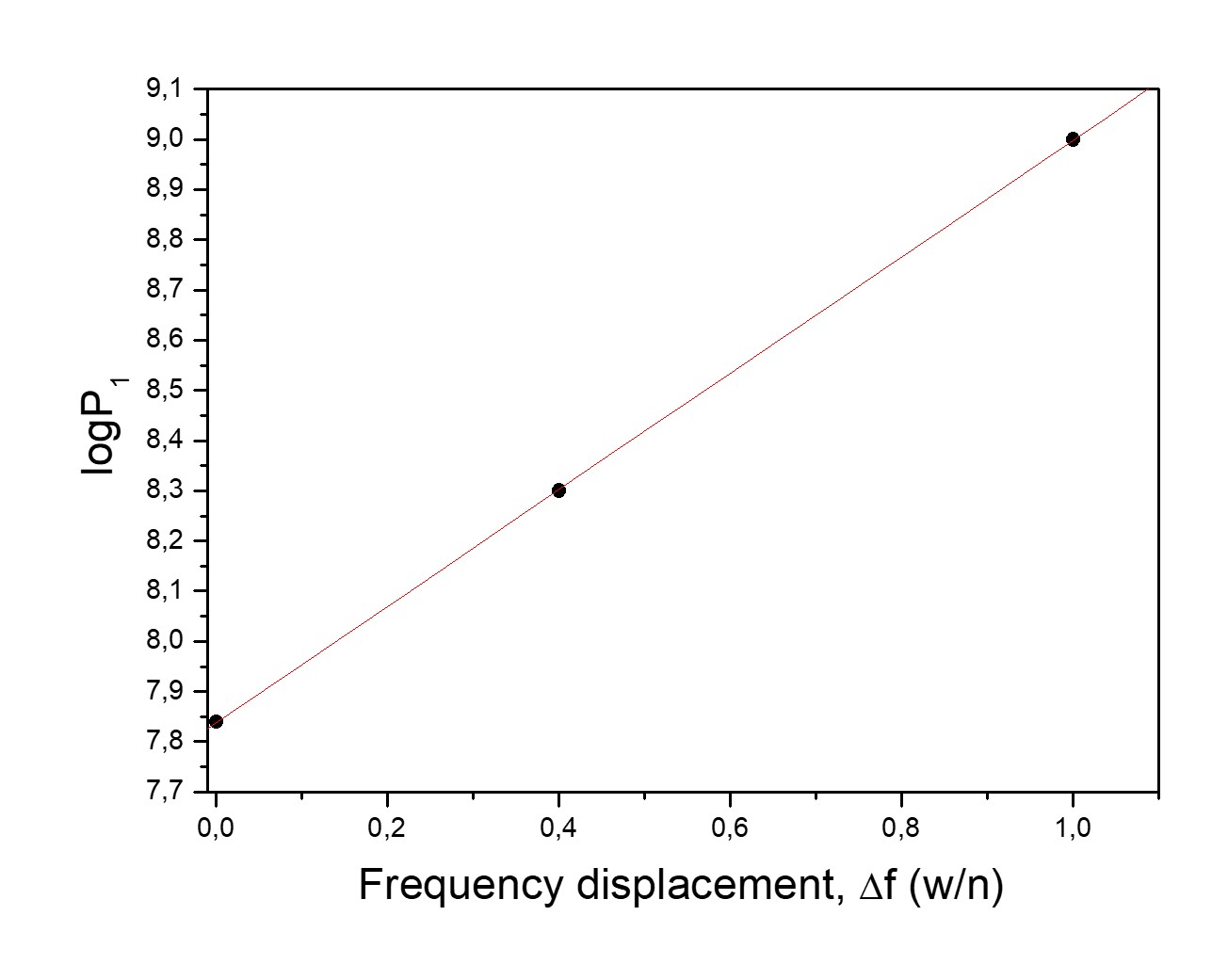
The logarithm of the spectral power at 1 wavenumber (P₁), equ. (1), in the double-slit experiment I reviewed in 2012, increases linearly with frequency shifts Δf between 0 and 1 wavenumbers. Shifting the spectrum to the right raises P₁ artificially due to the shape of the FFT spectrum at low frequencies. This directly affects the relative measure R = P(peak) / P₁, making it appear reduced according to the equation:

Graph (B). Relative Reduction in R.
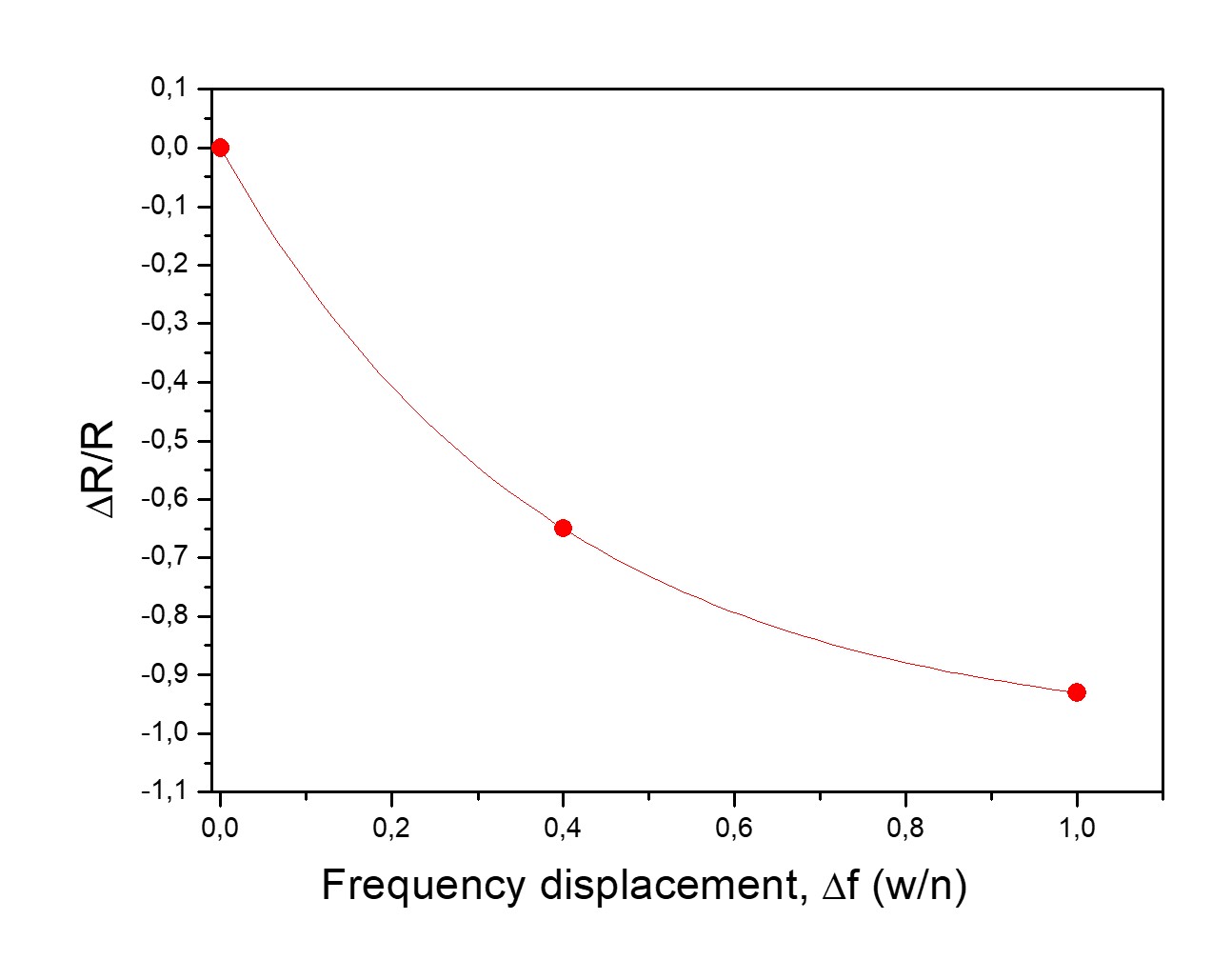
The relative change in R (ΔR/R), equ. (2), in the double-slit experiment I reviewed in 2012, shows an exponential decay with frequency shifts Δf between 0 and 1 wavenumbers. At Δf = 1 w/n, R drops by ~93%. This sensitivity underscores how even a small, deliberate shift in the FFT can produce the illusion of a dramatic experimental effect.

Graph (C). Exponential Decline in Fringe Visibility V.
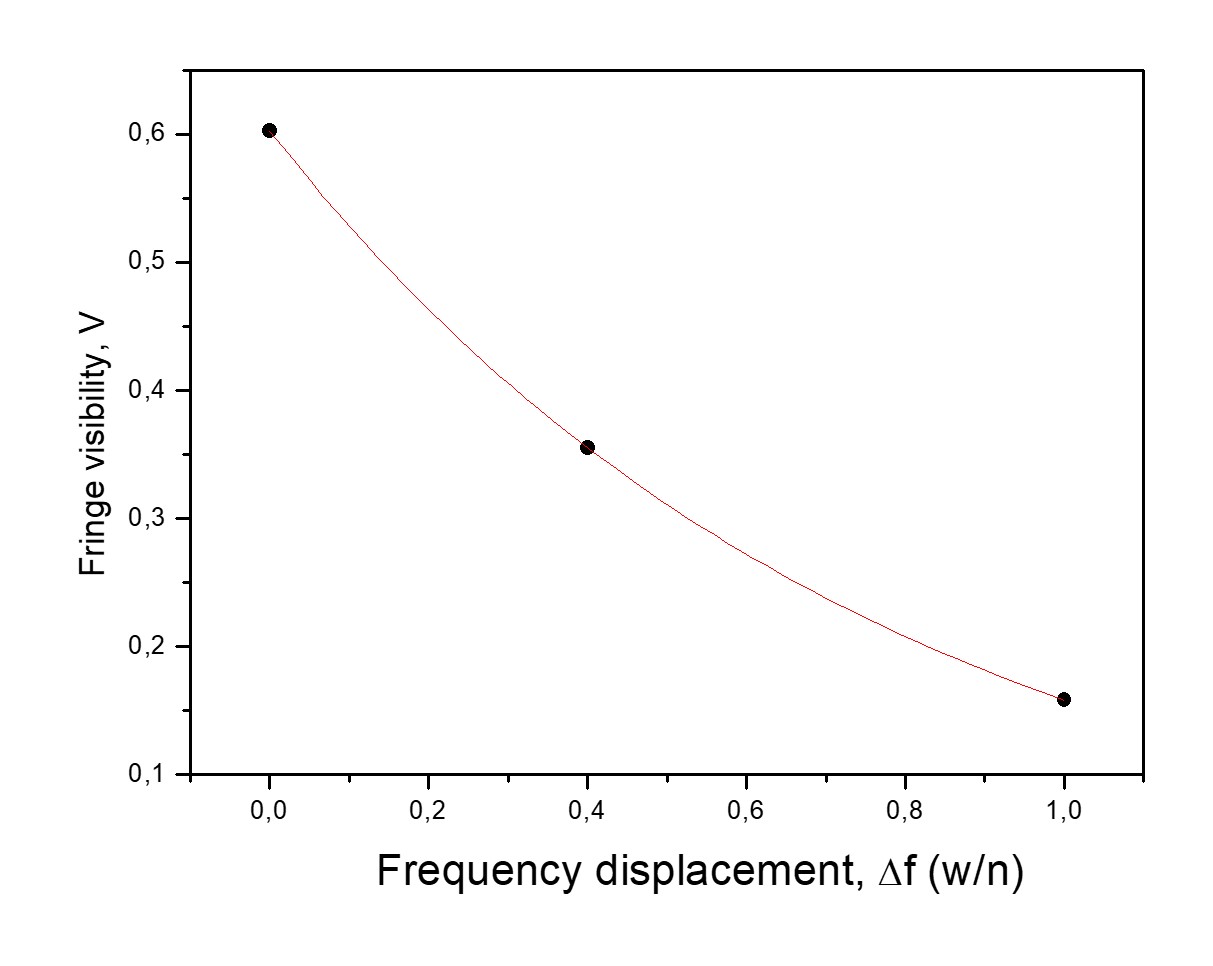
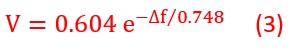
Fringe visibility V (defined as √R) in the double-slit experiment I reviewed in 2012, equ. (3), decays sharply as Δf increases. A shift of just 1 wavenumber reduces V from 0.60 to about 0.16, mimicking the alleged effect of mental intention. This suggests that the visibility change may be an artifact of spectral manipulation, not a physical phenomenon.
Note: Estimating equation (1) on the reported interference pattern of the double-slit experiment I reviewed in 2012 and the fitting of data in graphs (B) and (C) were performed using Origin Pro® 7.5
CONCLUSION
These graphs demonstrate that the key evidence reported in the double-slit experiment I reviewed in 2012—a reduction in spectral visibility allegedly attributed to consciousness—can be fully reproduced by an artificial shift of the FFT spectrum. The implications are significant: a modification of the spectrum by as little as one wavenumber is sufficient to simulate the central experimental claim.
How a Decrease in the Key Measure (R) Can Be Artificially Produced via Computer Programming
When the experimenter initiates a session intended to measure mental influence, the computer program responsible for generating the FFT spectrum may insert additional commands to shift the spectrum by a small, random offset Δf.
Mechanism Overview:
Step 1.After computing the FFT spectrum from the digitized camera signal, the program increases all frequency values by a random offset Δf, where Δf ∈ [0,1].
Step 2:This frequency shift displaces the entire spectrum, leaving a gap of width Δf near f = 0.
Step 3:A program command reads the spectral power at f = 1, now located further up the spectrum, where the power is higher due to the steep low-frequency slope. This becomes the new denominator, P'(1), in the key ratio R.
Step 4:The program also reads the power at the location of the main peak, now shifted to K+Δf. This becomes the new numerator, equal to the previous before the shift, P'(K+Δf), where K is known from the unshifted spectrum.
Step 5:The new, artificially reduced ratio is calculated as: (R') = P'(K+Δf) / P'(1).
Because P(1) increases after the shift while the numerator remains unchanged, the result is a lower R′—falsely suggesting a consciousness-induced effect.
Minimal Requirements for the Spectral Adjustment:
At the start of a mental-effort session, the program would need only three additional commands:
Replace f→f+Δf with Δf randomly selected in [0, 1],
Read the power at f = 1 on the shifted spectrum: P'(1).
Read the power at the main peak location on the shifted spectrum: P'(K+Δf),
Compute the new ratio: R′ = P'(K+Δf)/P'(1).
Programmers may be intrigued to simulate this themselves—it requires only a minor modification of standard FFT post-processing routines.
The telltale Spectral Gap
A visible frequency gap near zero frequency in the published FFT spectrum I reviewed in 2012 indicates the presence of a non-physical artifact. The absence of any comment or explanation regarding this feature reflects a lack of methodological clarity, similar to the inconsistencies in reported parameters such as the slit-to-camera distance and pixel size.
![Graph D: (A) Exponential decay of R with shift: R≈0.363∙e^(-Δf⁄0.37). Markers denote the unshifted condition (Δf = 0; R ≈ 0.363, ‘away’) and the shifted condition (Δf = 1; R ≈ 0.025, ‘towards’), corresponding to FFT recording sessions without and with attempted mental influence on the diffracted light, respectively. (B) Reinstated FFT spectrum. The 0–1 w/n region shows an approximately linear fall of spectral power, defining P1. (C) logP1 varies linearly with Δf∈[0,1], consistent with the exponential decay of R observed in panel A.](https://82840952b1.clvaw-cdnwnd.com/448d549c5aed8109384ccb84d1b9ed5e/200000389-a4f96a4f99/figure%203C-7.jpeg?ph=82840952b1)
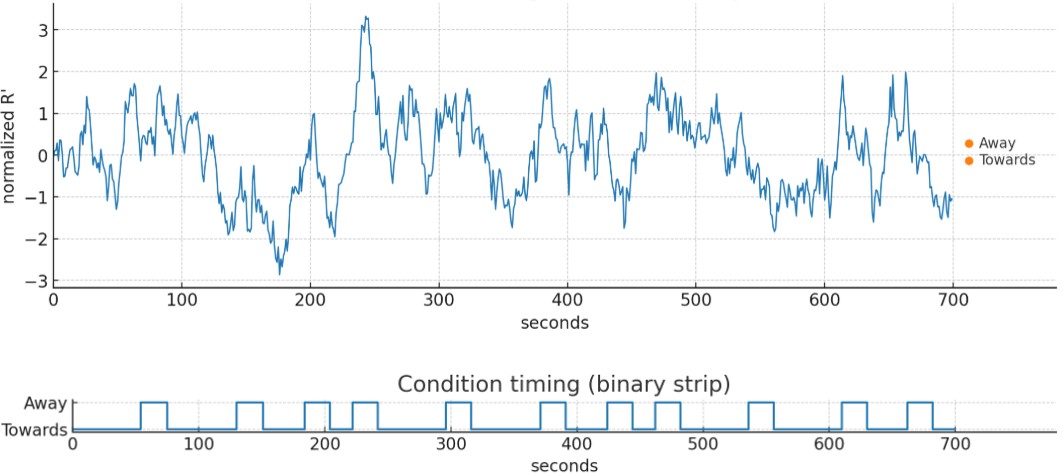
Graphs D & E: Injecting mixed spectral shifts (Δf ∈ [0,1]) into the FFT power-spectrum—Δf = 0 for the away condition and up to one frequency unit for the towards condition—across varying durations is sufficient to reproduce the reported difference in the normalized R measure. This simulation recovers the same effect size as described in the 2012 double-slit diffraction experiments I examined.
This simulation shows that the effect size reported in the 2012 double-slit diffraction experiments is explainable without invoking a consciousness-related effect on physical reality.